Class for second type Chebyshev-Gauss quadrature rule for one-dimensional functions. More...

#include <1DQuadrature.h>

Inheritance diagram for QUESO::WignerChebyshev2nd1DQuadrature:

Collaboration diagram for QUESO::WignerChebyshev2nd1DQuadrature:

Public Member Functions
Constructor/Destructor methods
	WignerChebyshev2nd1DQuadrature (double minDomainValue, double maxDomainValue, unsigned int order)
	Default constructor. More...

	~WignerChebyshev2nd1DQuadrature ()
	Destructor. More...

Mathematical methods
void	dumbRoutine () const
	Bogus routine. More...

Public Member Functions inherited from QUESO::Base1DQuadrature
	Base1DQuadrature (double minDomainValue, double maxDomainValue, unsigned int order)
	Default constructor. More...

virtual	~Base1DQuadrature ()
	Virtual destructor. More...

double	minDomainValue () const
	Returns the minimum value of the domain of the (one-dimensional) function. More...

double	maxDomainValue () const
	Returns the maximum value of the domain of the (one-dimensional) function. More...

unsigned int	order () const
	Returns the order of the quadrature rule. More...

const std::vector< double > &	positions () const
	Array of the positions for the numerical integration. More...

const std::vector< double > &	weights () const
	Array of the weights used in the numerical integration. More...

Additional Inherited Members
Protected Attributes inherited from QUESO::Base1DQuadrature
double	m_minDomainValue

double	m_maxDomainValue

unsigned int	m_order

std::vector< double >	m_positions

std::vector< double >	m_weights

Detailed Description

Class for second type Chebyshev-Gauss quadrature rule for one-dimensional functions.

Chebyshev-Gauss quadrature, also called Chebyshev Type 2 quadrature, is a Gaussian quadrature over the interval [-1,1] with weighting function 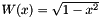$W(x)=\sqrt{1-x^2}$ .
The abscissas for quadrature order 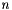$ n $ are given by the roots of the Chebyshev polynomial of the second kind 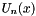$ U_n(x) $ , which occur symmetrically about 0.
The abscissas are given explicitly by $x_i=\cos[\frac{i\pi}{n+1}].$ and all the weights are $w_i=\frac{\pi}{n+1}\sin^2[\frac{i\pi}{n+1}].$

See Also: Weisstein, Eric W. "Gaussian Quadrature." From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/GaussianQuadrature.html.; http://en.wikipedia.org/wiki/Chebyshev-Gauss_quadrature.

Definition at line 313 of file 1DQuadrature.h.

Constructor & Destructor Documentation

QUESO::WignerChebyshev2nd1DQuadrature::WignerChebyshev2nd1DQuadrature	(	double	minDomainValue,
		double	maxDomainValue,
		unsigned int	order
	)

Default constructor.

Constructs a Gaussian-Chebyshev quadrature (of second type) of order order, in the interval [minDomainValue,maxDomainValue]. This method scales the abscissas (positions) of the quadrature from the interval [-1,1] to [minDomainValue,maxDomainValue].

Definition at line 694 of file 1DQuadrature.C.

References QUESO::Base1DQuadrature::m_maxDomainValue, QUESO::Base1DQuadrature::m_minDomainValue, QUESO::Base1DQuadrature::m_order, QUESO::Base1DQuadrature::m_positions, and QUESO::Base1DQuadrature::m_weights.

   :
   Base1DQuadrature(minDomainValue,maxDomainValue,order)
 {
   m_positions.resize(m_order+1,0.); // Yes, '+1'
   m_weights.resize  (m_order+1,0.); // Yes, '+1'
 
   // http://en.wikipedia.org/wiki/Chebyshev-Gauss_quadrature
   unsigned int n = m_order+1;
   for (unsigned int i = 0; i < n; ++i) {
     double angle = M_PI*((double)(i+1))/((double)(n+1));
     double cosValue = cos(angle);
     double sinValue = sin(angle);
     m_positions[i] = cosValue;
     m_weights[i] = ( M_PI/((double)(n+1)) )*sinValue*sinValue;
   }
 
   // Scale positions from the interval [-1, 1] to the interval [min,max]
   for (unsigned int j = 0; j < m_positions.size(); ++j) {
     m_positions[j] = .5*(m_maxDomainValue - m_minDomainValue)*m_positions[j] + .5*(m_maxDomainValue + m_minDomainValue);
     m_weights[j] *= .5*(m_maxDomainValue - m_minDomainValue);
   }
 }

QUESO::WignerChebyshev2nd1DQuadrature::~WignerChebyshev2nd1DQuadrature ( )

Destructor.

Definition at line 721 of file 1DQuadrature.C.

722 {

723 }

Member Function Documentation

void QUESO::WignerChebyshev2nd1DQuadrature::dumbRoutine ( ) const

virtual

Bogus routine.

Implements QUESO::Base1DQuadrature.

Definition at line 726 of file 1DQuadrature.C.

 {
   return;
 }

The documentation for this class was generated from the following files:

src/misc/inc/1DQuadrature.h
src/misc/src/1DQuadrature.C

Public Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation