queso-0.53.0
Protected Attributes | List of all members
QUESO::GaussianHermite1DQuadrature Class Reference

Class for Hermite-Gauss quadrature rule for one-dimensional functions. More...

#include <1DQuadrature.h>

Inheritance diagram for QUESO::GaussianHermite1DQuadrature:
Inheritance graph
[legend]
Collaboration diagram for QUESO::GaussianHermite1DQuadrature:
Collaboration graph
[legend]

Public Member Functions

Constructor/Destructor methods
 GaussianHermite1DQuadrature (double mean, double stddev, unsigned int order)
 Default constructor. More...
 
 ~GaussianHermite1DQuadrature ()
 Destructor. More...
 
Mathematical methods
void dumbRoutine () const
 A bogus method. More...
 
- Public Member Functions inherited from QUESO::Base1DQuadrature
 Base1DQuadrature (double minDomainValue, double maxDomainValue, unsigned int order)
 Default constructor. More...
 
virtual ~Base1DQuadrature ()
 Virtual destructor. More...
 
double minDomainValue () const
 Returns the minimum value of the domain of the (one-dimensional) function. More...
 
double maxDomainValue () const
 Returns the maximum value of the domain of the (one-dimensional) function. More...
 
unsigned int order () const
 Returns the order of the quadrature rule. More...
 
const std::vector< double > & positions () const
 Array of the positions for the numerical integration. More...
 
const std::vector< double > & weights () const
 Array of the weights used in the numerical integration. More...
 

Protected Attributes

double m_mean
 
double m_stddev
 
- Protected Attributes inherited from QUESO::Base1DQuadrature
double m_minDomainValue
 
double m_maxDomainValue
 
unsigned int m_order
 
std::vector< double > m_positions
 
std::vector< double > m_weights
 

Detailed Description

Class for Hermite-Gauss quadrature rule for one-dimensional functions.

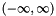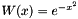Hermite-Gauss quadrature, also called Hermite quadrature, is a Gaussian quadrature over the interval $(-\infty,\infty)$ with weighting function $ W(x)=e^{-x^2}$.
The abscissas for quadrature order 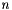$ n $ are given by the roots 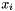$ x_i $ of the Hermite polynomials 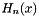$ H_n(x)$, which occur symmetrically about 0.
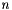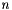The abscissas and weights can be computed analytically for small $ n $:

$ n $$ x_i $$ w_i $
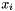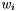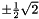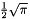2 $\pm \frac{1}{2}\sqrt{2} $ $ \frac{1}{2}\sqrt{\pi} $
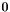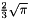3 $ 0 $ $ \frac{2}{3}\sqrt{\pi} $
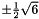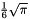$\pm \frac{1}{2}\sqrt{6} $ $ \frac{1}{6}\sqrt{\pi} $
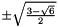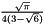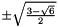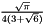4 $\pm \sqrt{\frac{3-\sqrt{6}}{2}} $ $ \frac{\sqrt{\pi}}{4(3-\sqrt{6})} $
$\pm \sqrt{\frac{3-\sqrt{6}}{2}} $ $ \frac{\sqrt{\pi}}{4(3+\sqrt{6})} $
See Also
Weisstein, Eric W. "Hermite-Gauss Quadrature." From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/Hermite-GaussQuadrature.html.

Definition at line 219 of file 1DQuadrature.h.

Constructor & Destructor Documentation

QUESO::GaussianHermite1DQuadrature::GaussianHermite1DQuadrature ( double  mean,
double  stddev,
unsigned int  order 
)

Default constructor.

Constructs a Gaussian-Hermite quadrature of order order. Valid values for the order of the quadrature rule are: 1-9, 19.

Todo:
: Prepare the code to include both parameters mean and stddev.

Definition at line 428 of file 1DQuadrature.C.

References QUESO::Base1DQuadrature::m_order, QUESO::Base1DQuadrature::m_positions, QUESO::Base1DQuadrature::m_weights, and queso_error_msg.

432  :
433  Base1DQuadrature(-INFINITY,INFINITY,order),
434  m_mean (mean),
435  m_stddev(stddev)
436 {
437  // FIX ME: prepare code for mean != 0 and stddev != 1
438  m_positions.resize(m_order+1,0.); // Yes, '+1'
439  m_weights.resize (m_order+1,0.); // Yes, '+1'
440 
441  // http://www.efunda.com/math/num_integration/findgausshermite.cfm
442  switch (m_order) { // eep2011
443  case 1:
444  m_weights [0] = sqrt(M_PI)/2.;
445  m_weights [1] = sqrt(M_PI)/2.;
446 
447  m_positions[0] = -1./sqrt(2.);
448  m_positions[1] = 1./sqrt(2.);
449  break;
450 
451  case 2:
452  m_weights [0] = sqrt(M_PI)/6.;
453  m_weights [1] = 2.*sqrt(M_PI)/3.;
454  m_weights [2] = sqrt(M_PI)/6.;
455 
456  m_positions[0] = -sqrt(1.5);
457  m_positions[1] = 0.;
458  m_positions[2] = sqrt(1.5);
459  break;
460 
461  case 3:
462  m_weights [0] = sqrt(M_PI)/4./(3.-sqrt(6.));
463  m_weights [1] = sqrt(M_PI)/4./(3.+sqrt(6.));
464  m_weights [2] = sqrt(M_PI)/4./(3.+sqrt(6.));
465  m_weights [3] = sqrt(M_PI)/4./(3.-sqrt(6.));
466 
467  m_positions[0] = -sqrt(1.5+sqrt(1.5));
468  m_positions[1] = -sqrt(1.5-sqrt(1.5));
469  m_positions[2] = sqrt(1.5-sqrt(1.5));
470  m_positions[3] = sqrt(1.5+sqrt(1.5));
471  break;
472 
473  case 4:
474  m_weights [0] = 0.019953242049;
475  m_weights [1] = 0.393619323152;
476  m_weights [2] = 0.945308720483;
477  m_weights [3] = 0.393619323152;
478  m_weights [4] = 0.019953242059;
479 
480  m_positions[0] = -sqrt(2.5+sqrt(2.5));
481  m_positions[1] = -sqrt(2.5-sqrt(2.5));
482  m_positions[2] = 0.;
483  m_positions[3] = sqrt(2.5-sqrt(2.5));
484  m_positions[4] = sqrt(2.5+sqrt(2.5));
485  break;
486 
487  case 5:
488  m_weights [0] = 0.00453000990551;
489  m_weights [1] = 0.157067320323;
490  m_weights [2] = 0.724629595224;
491  m_weights [3] = 0.724629595224;
492  m_weights [4] = 0.157067320323;
493  m_weights [5] = 0.00453000990551;
494 
495  m_positions [0] = -2.35060497367;
496  m_positions [1] = -1.33584907401;
497  m_positions [2] = -0.436077411928;
498  m_positions [3] = 0.436077411928;
499  m_positions [4] = 1.33584907401;
500  m_positions [5] = 2.35060497367;
501  break;
502 
503  case 6:
504  m_weights [0] = 0.0009717812451;
505  m_weights [1] = 0.0545155828191;
506  m_weights [2] = 0.42560725261;
507  m_weights [3] = 0.810264617557;
508  m_weights [4] = 0.42560725261;
509  m_weights [5] = 0.0545155828191;
510  m_weights [6] = 0.0009717812451;
511 
512  m_positions [0] = -2.65196135684;
513  m_positions [1] = -1.67355162877;
514  m_positions [2] = -0.816287882859;
515  m_positions [3] = 0.;
516  m_positions [4] = 0.816287882859;
517  m_positions [5] = 1.67355162877;
518  m_positions [6] = 2.65196135684;
519  break;
520 
521  case 7:
522  m_weights [0] = 0.000199604072211;
523  m_weights [1] = 0.0170779830074;
524  m_weights [2] = 0.207802325815;
525  m_weights [3] = 0.661147012558;
526  m_weights [4] = 0.661147012558;
527  m_weights [5] = 0.207802325815;
528  m_weights [6] = 0.0170779830074;
529  m_weights [7] = 0.000199604072211;
530 
531  m_positions [0] = -2.93063742026;
532  m_positions [1] = -1.9816567567;
533  m_positions [2] = -1.15719371245;
534  m_positions [3] = -0.381186990207;
535  m_positions [4] = 0.381186990207;
536  m_positions [5] = 1.15719371245;
537  m_positions [6] = 1.9816567567;
538  m_positions [7] = 2.93063742026;
539  break;
540 
541  case 8:
542  m_weights [0] = 3.96069772633e-5;
543  m_weights [1] = 0.00494362427554;
544  m_weights [2] = 0.0884745273944;
545  m_weights [3] = 0.432651559003;
546  m_weights [4] = 0.720235215606;
547  m_weights [5] = 0.432651559003;
548  m_weights [6] = 0.0884745273944;
549  m_weights [7] = 0.00494362427554;
550  m_weights [8] = 3.96069772633e-5;
551 
552  m_positions [0] = -3.19099320178;
553  m_positions [1] = -2.26658058453;
554  m_positions [2] = -1.46855328922;
555  m_positions [3] = -0.723551018753;
556  m_positions [4] = 0.;
557  m_positions [5] = 0.723551018753;
558  m_positions [6] = 1.46855328922;
559  m_positions [7] = 2.26658058453;
560  m_positions [8] = 3.19099320178;
561  break;
562 
563  case 9:
564  m_weights [0] = 7.64043285523e-6;
565  m_weights [1] = 0.00134364574678;
566  m_weights [2] = 0.0338743944555;
567  m_weights [3] = 0.240138611082;
568  m_weights [4] = 0.610862633735;
569  m_weights [5] = 0.610862633735;
570  m_weights [6] = 0.240138611082;
571  m_weights [7] = 0.0338743944555;
572  m_weights [8] = 0.00134364574678;
573  m_weights [9] = 7.64043285523e-6;
574 
575  m_positions [0] = -3.43615911884;
576  m_positions [1] = -2.53273167423;
577  m_positions [2] = -1.7566836493;
578  m_positions [3] = -1.03661082979;
579  m_positions [4] = -0.342901327224;
580  m_positions [5] = 0.342901327224;
581  m_positions [6] = 1.03661082979;
582  m_positions [7] = 1.7566836493;
583  m_positions [8] = 2.53273167423;
584  m_positions [9] = 3.43615911884;
585  break;
586 
587  case 19:
588  m_weights [0] = 2.22939364554e-13;
589  m_weights [1] = 4.39934099226e-10;
590  m_weights [2] = 1.08606937077e-7;
591  m_weights [3] = 7.8025564785e-6;
592  m_weights [4] = 0.000228338636017;
593  m_weights [5] = 0.00324377334224;
594  m_weights [6] = 0.0248105208875;
595  m_weights [7] = 0.10901720602;
596  m_weights [8] = 0.286675505363;
597  m_weights [9] = 0.462243669601;
598  m_weights [10] = 0.462243669601;
599  m_weights [11] = 0.286675505363;
600  m_weights [12] = 0.10901720602;
601  m_weights [13] = 0.0248105208875;
602  m_weights [14] = 0.00324377334224;
603  m_weights [15] = 0.000228338636017;
604  m_weights [16] = 7.8025564785e-6;
605  m_weights [17] = 1.08606937077e-7;
606  m_weights [18] = 4.39934099226e-10;
607  m_weights [19] = 2.22939364554e-13;
608 
609  m_positions [0] = -5.38748089001;
610  m_positions [1] = -4.60368244955;
611  m_positions [2] = -3.94476404012;
612  m_positions [3] = -3.34785456738;
613  m_positions [4] = -2.78880605843;
614  m_positions [5] = -2.25497400209;
615  m_positions [6] = -1.73853771212;
616  m_positions [7] = -1.2340762154;
617  m_positions [8] = -0.737473728545;
618  m_positions [9] = -0.245340708301;
619  m_positions[10] = 0.245340708301;
620  m_positions[11] = 0.737473728545;
621  m_positions[12] = 1.2340762154;
622  m_positions[13] = 1.73853771212;
623  m_positions[14] = 2.25497400209;
624  m_positions[15] = 2.78880605843;
625  m_positions[16] = 3.34785456738;
626  m_positions[17] = 3.94476404012;
627  m_positions[18] = 4.60368244955;
628  m_positions[19] = 5.38748089001;
629  break;
630 
631  default:
632  std::cerr << "In GaussianHermite1DQuadrature::constructor()"
633  << ": m_order = " << m_order
634  << std::endl;
635  queso_error_msg("order not supported");
636  break;
637  }
638  for (unsigned int j = 0; j < (m_order+1); ++j) {
639  m_weights [j] *= sqrt(2.);
640  m_positions[j] *= sqrt(2.);
641  }
642 }
QUESO::Base1DQuadrature::m_positions
std::vector< double > m_positions
Definition: 1DQuadrature.h:85
QUESO::Base1DQuadrature::order
unsigned int order() const
Returns the order of the quadrature rule.
Definition: 1DQuadrature.C:67
queso_error_msg
#define queso_error_msg(msg)
Definition: asserts.h:47
QUESO::Base1DQuadrature::Base1DQuadrature
Base1DQuadrature(double minDomainValue, double maxDomainValue, unsigned int order)
Default constructor.
Definition: 1DQuadrature.C:32
QUESO::Base1DQuadrature::m_weights
std::vector< double > m_weights
Definition: 1DQuadrature.h:86
QUESO::GaussianHermite1DQuadrature::~GaussianHermite1DQuadrature ( )

Destructor.

Definition at line 644 of file 1DQuadrature.C.

645 {
646 }

Member Function Documentation

void QUESO::GaussianHermite1DQuadrature::dumbRoutine ( ) const
virtual

A bogus method.

Implements QUESO::Base1DQuadrature.

Definition at line 649 of file 1DQuadrature.C.

650 {
651  return;
652 }

Member Data Documentation

double QUESO::GaussianHermite1DQuadrature::m_mean
protected

Definition at line 246 of file 1DQuadrature.h.

double QUESO::GaussianHermite1DQuadrature::m_stddev
protected

Definition at line 247 of file 1DQuadrature.h.

The documentation for this class was generated from the following files:
Generated on Thu Jun 11 2015 13:52:35 for queso-0.53.0 by  doxygen 1.8.5