Class for one-dimensional Lagrange polynomials. More...
#include <1D1DFunction.h>
Public Member Functions | |
Constructor/Destructor methods | |
| LagrangePolynomial1D1DFunction (const std::vector< double > &positionValues, const std::vector< double > *functionValues) | |
| Default constructor. More... | |
| ~LagrangePolynomial1D1DFunction () | |
| Destructor. More... | |
Mathematical methods | |
| double | value (double domainValue) const |
Returns the value of the Lagrange polynomial at point domainValue. More... | |
| double | deriv (double domainValue) const |
TODO: Returns the value of the derivative of the Lagrange polynomial at point domainValue. More... | |
 Public Member Functions inherited from QUESO::Base1D1DFunction Public Member Functions inherited from QUESO::Base1D1DFunction | |
| Base1D1DFunction (double minDomainValue, double maxDomainValue) | |
| Default constructor. More... | |
| virtual | ~Base1D1DFunction () |
| Destructor. More... | |
| double | minDomainValue () const |
| Returns the minimum value of the domain of the (one-dimensional) function. More... | |
| double | maxDomainValue () const |
| Returns the maximum value of the domain of the (one-dimensional) function. More... | |
| virtual double | multiplyAndIntegrate (const Base1D1DFunction &func, unsigned int quadratureOrder, double *resultWithMultiplicationByTAsWell) const |
TODO: Multiplies this function with function, and integrates it numerically. See template specialization. More... | |
Protected Attributes | |
| std::vector< double > | m_positionValues |
| std::vector< double > | m_functionValues |
 Protected Attributes inherited from QUESO::Base1D1DFunction Protected Attributes inherited from QUESO::Base1D1DFunction | |
| double | m_minDomainValue |
| double | m_maxDomainValue |
Detailed Description
Class for one-dimensional Lagrange polynomials.
The Lagrange interpolating polynomial of a one-dimensional function 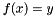 is the polynomial
is the polynomial 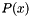 of degree
of degree 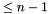 that passes through the
that passes through the 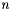 points
points 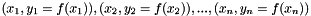 , and is given by:
, and is given by:
![\[ P(x)=\sum_{j=1}^n \prod_{k=1; k\not=j}^n \frac{x-x_k}{x_j-x_k}.\]](form_9.png)
Written explicitly,
![\[ P(x)=\frac{(x-x_2)(x-x_3)...(x-x_n)}{(x_1-x_2)(x_1-x_3)...(x_1-x_n)}y_1+ \frac{(x-x_1)(x-x_3)...(x-x_n)}{(x_2-x_1)(x_2-x_3)...(x_2-x_n)}y_2+...+ \frac{(x-x_1)(x-x_2)...(x-x_(n-1))}{(x_n-x_1)(x_n-x_2)...(x_n-x_(n-1))}y_n.\]](form_10.png)
In this class, the array std::vector<double>& positionValues stores the points 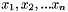 and the array
and the array std::vector<double>* functionValues stores the points 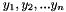 of the Lagrange polynomial.
of the Lagrange polynomial.
- See Also
- Archer, Branden and Weisstein, Eric W. "Lagrange Interpolating Polynomial." From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html.
Definition at line 558 of file 1D1DFunction.h.
Constructor & Destructor Documentation
| QUESO::LagrangePolynomial1D1DFunction::LagrangePolynomial1D1DFunction | ( | const std::vector< double > & | positionValues, |
| const std::vector< double > * | functionValues | ||
| ) |
Default constructor.
Definition at line 827 of file 1D1DFunction.C.
References m_functionValues, m_positionValues, UQ_FATAL_TEST_MACRO, and QUESO::UQ_UNAVAILABLE_RANK.
| QUESO::LagrangePolynomial1D1DFunction::~LagrangePolynomial1D1DFunction | ( | ) |
Member Function Documentation
|
virtual |
TODO: Returns the value of the derivative of the Lagrange polynomial at point domainValue.
- Todo:
- This function checks if point
domainValuebelongs to the domain ofthisfunction, and in affirmative case, it returns the value of the derivative at such point.
Implements QUESO::Base1D1DFunction.
Definition at line 884 of file 1D1DFunction.C.
References QUESO::Base1D1DFunction::m_maxDomainValue, QUESO::Base1D1DFunction::m_minDomainValue, UQ_FATAL_TEST_MACRO, QUESO::UQ_UNAVAILABLE_RANK, and value().
|
virtual |
Returns the value of the Lagrange polynomial at point domainValue.
Implements QUESO::Base1D1DFunction.
Definition at line 849 of file 1D1DFunction.C.
References m_functionValues, and m_positionValues.
Referenced by deriv().
Member Data Documentation
|
protected |
Definition at line 585 of file 1D1DFunction.h.
Referenced by LagrangePolynomial1D1DFunction(), and value().
|
protected |
Definition at line 584 of file 1D1DFunction.h.
Referenced by LagrangePolynomial1D1DFunction(), and value().
The documentation for this class was generated from the following files:
- src/misc/inc/1D1DFunction.h
- src/misc/src/1D1DFunction.C