Linear Lagrange interpolation surrogate. More...

#include <LinearLagrangeInterpolationSurrogate.h>

Inheritance diagram for QUESO::LinearLagrangeInterpolationSurrogate< V, M >:

Public Member Functions
	LinearLagrangeInterpolationSurrogate (const InterpolationSurrogateData< V, M > &data)
	Constructor. More...

virtual	~LinearLagrangeInterpolationSurrogate ()

virtual double	evaluate (const V &domainVector) const
	Evaluates value of the interpolant for the given domainVector. More...

unsigned int	n_coeffs () const
	The number of coeffs for interpolating. More...

Public Member Functions inherited from QUESO::InterpolationSurrogateBase< V, M >
	InterpolationSurrogateBase (const InterpolationSurrogateData< V, M > &data)
	Constructor. More...

virtual	~InterpolationSurrogateBase ()

Public Member Functions inherited from QUESO::SurrogateBase< V >
	SurrogateBase ()

virtual	~SurrogateBase ()

Protected Member Functions
void	compute_interval_indices (const V &domainVector, std::vector< unsigned int > &indices) const
	Helper function to get lower bound indices for each dimension. More...

void	compute_interval_values (const std::vector< unsigned int > &indices, std::vector< double > &x_min, std::vector< double > &x_max, std::vector< double > &values) const
	Helper function to populate bounding values for the intervals in each dimension. More...

double	eval_interpolant (const std::vector< double > &x_min, const std::vector< double > &x_max, const std::vector< double > &values, const V &domainVector) const
	Evaluate multidimensional linear Lagrange interpolant. More...

unsigned int	coordsToSingle (const std::vector< unsigned int > &indices) const
	Convert local indices to single "global" index. More...

void	singleToCoords (unsigned int global, std::vector< unsigned int > &indices) const
	Inverse of map computed in coordsToSingle. More...

double	tensor_product_lagrange (const std::vector< double > &x_min, const std::vector< double > &x_max, const std::vector< unsigned int > &indices, const V &domainVector) const
	Compute multidimensional Lagrange polynomial as tensor product of 1D polynomials. More...

double	lagrange_poly (double x0, double x1, double x, unsigned int index) const
	Evaluate a 1-D Lagrange polynomial at point x. More...

Private Member Functions
	LinearLagrangeInterpolationSurrogate ()

Additional Inherited Members
Protected Attributes inherited from QUESO::InterpolationSurrogateBase< V, M >
const InterpolationSurrogateData< V, M > &	m_data

Detailed Description

template<class V = GslVector, class M = GslMatrix>
class QUESO::LinearLagrangeInterpolationSurrogate< V, M >

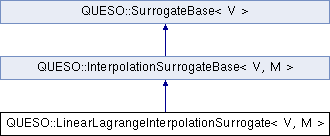
Linear Lagrange interpolation surrogate.

Aribritary dimension linear Lagrange interpolant. Uses a structured grid to interpolate values given by data passed to the constructor.

Definition at line 44 of file LinearLagrangeInterpolationSurrogate.h.

Constructor & Destructor Documentation

template<class V , class M >

QUESO::LinearLagrangeInterpolationSurrogate< V, M >::LinearLagrangeInterpolationSurrogate ( const InterpolationSurrogateData< V, M > & data )

Constructor.

The data object should be already fully populated when constructing this object. The user can directly set values or use the InterpolationSurrogateBuilder object to populate the data.

Definition at line 37 of file LinearLagrangeInterpolationSurrogate.C.

38 : InterpolationSurrogateBase<V,M>(data)

39 {}

template<class V = GslVector, class M = GslMatrix>

virtual QUESO::LinearLagrangeInterpolationSurrogate< V, M >::~LinearLagrangeInterpolationSurrogate ( )

inlinevirtual

Definition at line 54 of file LinearLagrangeInterpolationSurrogate.h.

54 {};

template<class V = GslVector, class M = GslMatrix>

QUESO::LinearLagrangeInterpolationSurrogate< V, M >::LinearLagrangeInterpolationSurrogate ( )

private

Member Function Documentation

template<class V , class M >

void QUESO::LinearLagrangeInterpolationSurrogate< V, M >::compute_interval_indices	(	const V &	domainVector,
		std::vector< unsigned int > &	indices
	)		const

protected

Helper function to get lower bound indices for each dimension.

domainVector contains the current value at which want want to interpolate. We use that to figure out the bounding values in each dimension. Then we populate indices with the lower index.

Definition at line 66 of file LinearLagrangeInterpolationSurrogate.C.

   {
     queso_assert_equal_to( domainVector.sizeGlobal(), this->m_data.dim() );
     queso_assert_equal_to( indices.size(), this->m_data.dim() );
 
     for( unsigned int d = 0; d < this->m_data.dim(); d++ )
       {
         double spacing = this->m_data.spacing(d);
         indices[d] = std::floor( (domainVector[d] - this->m_data.x_min(d))/spacing );
 
         // Index should be less than the number of point along this dimension
         queso_assert_less( indices[d], this->m_data.get_n_points()[d] );
       }
   }

template<class V , class M >

void QUESO::LinearLagrangeInterpolationSurrogate< V, M >::compute_interval_values	(	const std::vector< unsigned int > &	indices,
		std::vector< double > &	x_min,
		std::vector< double > &	x_max,
		std::vector< double > &	values
	)		const

protected

Helper function to populate bounding values for the intervals in each dimension.

By convention, it is assumed that the indices vector contains the lower bound index. See compute_interval_indices.

Definition at line 83 of file LinearLagrangeInterpolationSurrogate.C.

References QUESO::MultiDimensionalIndexing::coordToGlobal().

   {
     queso_assert_equal_to( x_min.size(), this->m_data.dim() );
     queso_assert_equal_to( x_max.size(), this->m_data.dim() );
     queso_assert_equal_to( values.size(), this->n_coeffs() );
     queso_assert_equal_to( indices.size(), this->m_data.dim() );
 
     // First, use the lower bound (global) indices to populate x_min, x_max
     for( unsigned int d = 0; d < this->m_data.dim(); d++ )
       {
         x_min[d] = this->m_data.get_x( d, indices[d] );
         x_max[d] = x_min[d] + this->m_data.spacing( d );
       }
 
     // Now populate the values.
     std::vector<unsigned int> local_indices(this->m_data.dim());
     std::vector<unsigned int> global_indices(this->m_data.dim());
     for( unsigned int n = 0 ; n < this->n_coeffs(); n++ )
       {
         // Figure out local indices (each coordinate is 0 or 1)
         this->singleToCoords(n,local_indices);
 
         /* For each dimension, if the local index is 0, use the lower
            bound of the global index. If the local index is 1, use the
            "upper" global index.
 
            In 2-D:
            The lower left corner of the element will have local_indices = [0,0];
            Then, global_indices = [ indices[0], indices[1] ];
            The upper right corner will have local_indices = [1,1];
            Then, global_indices = [ indices[0]+1, indices[1]+1 ]; */
         for( unsigned int d = 0; d < this->m_data.dim(); d++ )
           {
             if( local_indices[d] == 0 )
               global_indices[d] = indices[d];
 
             else if( local_indices[d] == 1 )
               global_indices[d] = indices[d]+1;
 
             // This shouldn't happen
             else
               queso_error();
           }
 
         /* Now that we have the global indices for each coordinate,
            we get the "global" index. This is the index into the global
            values array */
         unsigned int global = MultiDimensionalIndexing::coordToGlobal( global_indices, this->m_data.get_n_points() );
         values[n] = this->m_data.get_value(global);
       }
   }

template<class V , class M >

unsigned int QUESO::LinearLagrangeInterpolationSurrogate< V, M >::coordsToSingle ( const std::vector< unsigned int > & indices ) const

protected

Convert local indices to single "global" index.

This is for handling the local ordering of an arbitrary dimensional linear Lagrange elements. The function will look like \( \sum_{ijkl...} f_{ijkl...} N_{ijkl...} \) so we want a convenient way to map \( ijkl... \) to a single integer. Then, we can order all our data this way and easily index into it. We can do this since each of \( ijkl... \) is either 0 or 1.

Definition at line 166 of file LinearLagrangeInterpolationSurrogate.C.

References QUESO::MultiDimensionalIndexing::coordToGlobal().

   {
     unsigned int local_dim = 2;
     std::vector<unsigned int> n_points( this->m_data.dim(), local_dim );
 
     /* We're abusing this function as it does what we need to with local_dim = 2
        for all entries of n_points. */
     return MultiDimensionalIndexing::coordToGlobal( indices, n_points );
   }

template<class V , class M >

double QUESO::LinearLagrangeInterpolationSurrogate< V, M >::eval_interpolant	(	const std::vector< double > &	x_min,
		const std::vector< double > &	x_max,
		const std::vector< double > &	values,
		const V &	domainVector
	)		const

protected

Evaluate multidimensional linear Lagrange interpolant.

This is just a tensor product of one-dimensional interpolants

Definition at line 139 of file LinearLagrangeInterpolationSurrogate.C.

   {
     queso_assert_equal_to( x_min.size(), this->m_data.dim() );
     queso_assert_equal_to( x_max.size(), this->m_data.dim() );
     queso_assert_equal_to( values.size(), this->n_coeffs() );
     queso_assert_equal_to( domainVector.sizeGlobal(), this->m_data.dim() );
 
     double interp_value = 0.0;
 
     std::vector<unsigned int> indices( this->m_data.dim() );
 
     for( unsigned int n = 0; n < this->n_coeffs(); n++ )
       {
         this->singleToCoords( n, indices );
 
         double shape_fn = this->tensor_product_lagrange( x_min, x_max, indices, domainVector );
 
         interp_value += values[n]*shape_fn;
       }
 
     return interp_value;
   }

template<class V , class M >

double QUESO::LinearLagrangeInterpolationSurrogate< V, M >::evaluate ( const V & domainVector ) const

virtual

Evaluates value of the interpolant for the given domainVector.

Implements QUESO::SurrogateBase< V >.

Definition at line 42 of file LinearLagrangeInterpolationSurrogate.C.

   {
     /* Populate indices. These are the lower bound global indices for the
        "element" containing the domainVector */
     std::vector<unsigned int> indices(this->m_data.dim());
     this->compute_interval_indices(domainVector, indices);
 
     // lower bound coordinates
     std::vector<double> x_min(this->m_data.dim());
 
     // upper bound coordinates
     std::vector<double> x_max(this->m_data.dim());
 
     // Function value at each of the "nodes" for the "element"
     std::vector<double> values(this->n_coeffs());
 
     // Use the indices to populate the x_min, etc. structures
     this->compute_interval_values( indices, x_min, x_max, values );
 
     // Now evaluate the interpolant
     return this->eval_interpolant( x_min, x_max, values, domainVector );
   }

template<class V , class M >

double QUESO::LinearLagrangeInterpolationSurrogate< V, M >::lagrange_poly	(	double	x0,
		double	x1,
		double	x,
		unsigned int	index
	)		const

protected

Evaluate a 1-D Lagrange polynomial at point x.

index tells us which of the two Lagrange functions to use. index must be 0 or 1.

Definition at line 209 of file LinearLagrangeInterpolationSurrogate.C.

   {
     // Make sure we're trying to interpolate between the given points
     queso_assert_less_equal( x, x1 );
     queso_assert_greater_equal( x, x0 );
 
     // Make sure index is either 0 or 1
     queso_assert( (index == 0) || (index == 1) );
 
     double value = 0.0;
 
     if( index == 0 )
       value = (x-x1)/(x0-x1);
     else
       value = (x-x0)/(x1-x0);
 
     return value;
   }

template<class V = GslVector, class M = GslMatrix>

unsigned int QUESO::LinearLagrangeInterpolationSurrogate< V, M >::n_coeffs ( ) const

inline

The number of coeffs for interpolating.

Definition at line 60 of file LinearLagrangeInterpolationSurrogate.h.

References QUESO::InterpolationSurrogateBase< V, M >::m_data.

61 { return std::pow( 2, this->m_data.dim() ); };

QUESO::InterpolationSurrogateBase::m_data

const InterpolationSurrogateData< V, M > & m_data

Definition: InterpolationSurrogateBase.h:62

template<class V , class M >

void QUESO::LinearLagrangeInterpolationSurrogate< V, M >::singleToCoords	(	unsigned int	global,
		std::vector< unsigned int > &	indices
	)		const

protected

Inverse of map computed in coordsToSingle.

Definition at line 177 of file LinearLagrangeInterpolationSurrogate.C.

References QUESO::MultiDimensionalIndexing::globalToCoord().

   {
     unsigned int local_dim = 2;
     std::vector<unsigned int> n_points( this->m_data.dim(), local_dim );
 
     /* We're abusing this function as it does what we need to with local_dim = 2
        for all entries of n_points. */
     return MultiDimensionalIndexing::globalToCoord( global, n_points, indices );
   }

template<class V , class M >

double QUESO::LinearLagrangeInterpolationSurrogate< V, M >::tensor_product_lagrange	(	const std::vector< double > &	x_min,
		const std::vector< double > &	x_max,
		const std::vector< unsigned int > &	indices,
		const V &	domainVector
	)		const

protected

Compute multidimensional Lagrange polynomial as tensor product of 1D polynomials.

\( N_{ijkl...} (\xi, \eta, \zeta,...) = N_i(\eta) N_j(\eta) N_k(\zeta) ... \) The indices vector contains the i,j,k,... values

Definition at line 188 of file LinearLagrangeInterpolationSurrogate.C.

   {
     queso_assert_equal_to( x_min.size(), this->m_data.dim() );
     queso_assert_equal_to( x_max.size(), this->m_data.dim() );
     queso_assert_equal_to( indices.size(), this->m_data.dim() );
     queso_assert_equal_to( domainVector.sizeGlobal(), this->m_data.dim() );
 
     double value = 1.0;
 
     for( unsigned int d = 0; d < this->m_data.dim(); d++ )
       {
         value *= this->lagrange_poly( x_min[d], x_max[d], domainVector[d], indices[d] );
       }
 
     return value;
   }

The documentation for this class was generated from the following files:

src/surrogates/inc/LinearLagrangeInterpolationSurrogate.h
src/surrogates/src/LinearLagrangeInterpolationSurrogate.C

Public Member Functions

Protected Member Functions

Private Member Functions

Additional Inherited Members

Detailed Description

template<class V = GslVector, class M = GslMatrix> class QUESO::LinearLagrangeInterpolationSurrogate< V, M >

Constructor & Destructor Documentation

Member Function Documentation

template<class V = GslVector, class M = GslMatrix>
class QUESO::LinearLagrangeInterpolationSurrogate< V, M >